¿Es posible predecir la distribución geográfica de las especies basándonos en variables ambientales?
Jorge M. Lobo
1. La cuestión
2. ¿Cuanto esfuerzo es suficiente?
3. Buscando la función predictiva
3.1 Necesidades.
3.2 Los inoportunos inconvenientes
3.3 Un ejemplo
4. Los factores históricos y el espacio
5. Comentario final
6. Bibliografía
1. - La cuestión
La disminución y desaparición de poblaciones y especies enteras debido a la perturbación ejercida sobre el medio por las actividades humanas, constituye uno de los conflictos ambientales más graves que debe enfrentar actualmente la humanidad (Wilson, 1988). Ante la magnitud e importancia del problema, parece adecuado recomendar que cualquier estrategia de protección de la biodiversidad deba sustentarse en evidencias científicas
(Murphy, 1990). Sin embargo, la comunidad científica sólo posee respuestas aproximadas sobre los procesos que generan y mantienen la diversidad biológica y es necesario, como paso preliminar ineludible, recopilar, compendiar y cartografiar la información biológica actualmente dispersa en la literatura y las colecciones. Esta colosal tarea necesita de una aproximación nueva que fusione y enlace las fronteras de disciplinas, a menudo separadas, como la Sistemática, la Biogeografía y la Ecología que, ante la denominada crisis de la biodiversidad, tienen la obligación de compartir objetivos y amalgamarse.
El estudio de las condiciones climáticas durante los dos últimos millones de años demuestra que el medio abiótico está en un permanente estado de no-equilibrio y que las condiciones ambientales siguen tendencias cambiantes de distinta duración. La respuesta de las especies ante esos cambios ha sido la dispersión sin apenas evidencias de modificaciones morfológicas importantes (Coope, 1979; Elias, 1994; Huntley & Birks, 1983; Webb et al., 1993). Si las especies son relativamente rígidas y si, además, el medio abiótico está en permanente estado de transformación, la reacción más eficaz de una especie ante una modificación ambiental consiste en variar espacialmente su distribución geográfica a fin de acoplar espacialmente los requerimientos eco-fisiológicos en aquellos enclaves que reproducen las condiciones ambientales para las que está adaptada (adaptación espacial; véase Hengeveld, 1997 y Lobo, 1999 para una revisión sobre el tema). Este modo de entender el medio natural concede gran importancia a la dimensión espacial y es de gran ayuda si queremos explicar la diversidad y la composición faunística de un determinado territorio. La Biogeografía se convierte así en una disciplina de alto valor explicativo a la hora de estudiar la variación espacial de la biodiversidad.
Actualmente, el estudio de la biogeografía de la biodiversidad tiene como principales objetivos:
- elaborar estrategias generales de inventario e identificación rápidas y eficaces
- obtener una información de base extensa mediante la compilación y cartografía del conocimiento disponible sobre la diversidad biológica
- buscar modelos capaces de predecir el número de especies u otra característica relacionada con la biodiversidad en ausencia de datos exhaustivos.
Las potentes herramientas informáticas disponibles, en especial los programas de bases de datos y los sistemas de información geográfica, facilitan enormemente la recopilación y cartografía de la información biológica (Davis, 1994; Margules & Austin, 1994; Miller, 1994; ver http://viceroy.eeb.uconn.edu/Biota). El análisis ulterior de esta información debe permitir evaluar el esfuerzo taxonómico y faunístico realizado, describir el emplazamiento de las áreas y los grupos taxonómicos necesitados de prospección, estimando el trabajo pendiente necesario para completar los atlas de la biodiversidad (véase Morrone en este mismo volumen). Sin embargo, son pocos los casos en los que se está acometiendo esta labor de manera permanente (Beaufort & Maurin, 1988; Harding & Sheail, 1992; ver también http://kaos.erin.gov.au (Environmental Resources Information Network, Australia), http://www.conabio.gob.mx (Comisión Nacional para el Conocimiento y el Uso de la Biodiversidad, México), o http://www.inbio.ac.cr (Instituto Nacional de Biodiversidad, Costa Rica) y muchos los lamentos sobre el poco esfuerzo dedicado a la recolección, determinación y estudio sistemático animal y vegetal, sobre todo en aquellos países económicamente pobres, pero ricos en número de especies y endemismos.
2. - ¿Cuanto esfuerzo es suficiente?
Cuantificar el esfuerzo de muestreo es imprescindible para evaluar la calidad de la información biológica disponible, pero no es sencillo determinar cuan completos son nuestros inventarios. Rara vez puede demostrarse que el incremento en el esfuerzo de muestreo de un territorio permite descubrir nuevas especies de un grupo cualquiera (Gaston, 1996). Sin embargo, los datos sobre la distribución de una especie se limitan a constatar su presencia, sin existir medida alguna que permita diferenciar la ausencia de la falta de muestreo. En los pocos casos en los que se manejan datos sobre la distribución geográfica del número de especies de un grupo, se evita mencionar generalmente que dicha información procede de diversas fuentes, es decir, que ha sido recogida utilizando distintos métodos y esfuerzos. De este modo, resulta imposible discernir cuál es el efecto de la variación en la intensidad de muestreo sobre la distribución del número de especies y, por tanto, cuál es el patrón real de distribución (Williams & Gaston, 1994). Algunas aproximaciones metodológicas permiten realizar comparaciones entre la riqueza de especies de distintas localidades, corrigiendo el número de especies de un área según el esfuerzo de muestreo realizado en ella (Hurlbert, 1971; Prendergast et al., 1993). Estas técnicas pretenden obtener estimas relativas comparables de riqueza entre distintas localidades, pero no ofrecen información sobre el número absoluto de especies que contienen. Sin embargo, para la aplicación de todas estas metodologías se necesitan siempre datos con un mínimo de calidad. Datos que ofrezcan información sobre la abundancia de las especies o que estén asociados con alguna medida de esfuerzo claramente definida. Cuando procede, éstas metodologías son muy valiosas pero, evidentemente, nada pueden hacer cuando el problema fundamental es la ausencia de información
Si el grado de conocimiento taxonómico y biogeográfico de un territorio es precario, el esfuerzo aún por realizar puede ser de tales proporciones, que resulta imposible obtener a medio plazo una aproximación fiable del reparto espacial del número de especies. Aunque resulte descorazonador, no hay que descartar que esta situación sea corriente incluso en aquellos grupos bien estudiados y en países con una prolongada tradición sistemática. Veamos un ejemplo.
Los coleópteros coprófagos de la subfamilia Scarabaeinae son uno de los grupos de insectos mejor estudiados en Europa Occidental. Tanto en la Península Ibérica como en Francia, existen bancos de datos exhaustivos que compendian toda la información museística y bibliográfica disponible (Lumaret., 1990; Lobo & Martín-Piera 1991). Utilizando como medida de esfuerzo la cantidad de registros contenidos en dichas bases de datos para cada cuadrícula UTM de 50 Km., se realizó un análisis de la relación asintótica entre el número de especies y el esfuerzo de muestreo (ver Soberón & Llorente 1993), expresado este como el número de registros (Figura 1).
|
|
|
Figura 1.- Relación entre el número de registros y el número de especies para cada cuadrícula UTM de 50 km según la información contenida en una exhaustiva base de datos sobre los Escarabeidos Ibéricos (arriba). Relación asintótica entre esas mismas variables para cada una de las regiones fisiográficas de la Península Ibérica (abajo). |
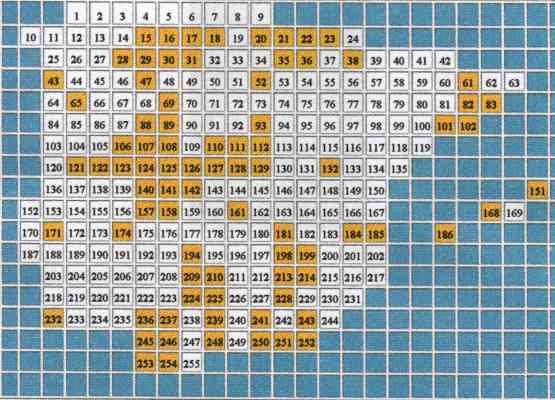
Dicho análisis demostró que únicamente entre un 25% y 32% del total de las cuadrículas pueden considerarse relativamente bien muestreadas (Figura 2).
|
|
|
Figura 2.- El mapa representa en color aquellas cuadrículas que pueden considerarse relativamente bien muestradas |
Es decir, recopilar durante años toda la información disponible desde hace más de un siglo, sobre un grupo faunística y taxonómicamente bien estudiado (la última nueva especie fue descrita hace más de 20 años), sólo permite tener inventarios fiables en apenas poco más de la cuarta parte del territorio. Considerando, además, que se trata de una escala espacial grosera (cuadrículas de unos 2.500 Km2 aproximadamente) y de un país europeo, ¿;cuál puede ser entonces la situación en otras áreas más ricas y con menor información almacenada?; ¿Qué podemos hacer entonces?
3. - Buscando la función predictiva.
En este caso, la única alternativa es realizar pronósticos razonables sobre la distribución del número de especies. La relación entre el número de taxones de alto rango y el número de especies, la búsqueda de especies indicadoras y la utilización de información ambiental de diverso tipo para obtener modelos con valor predictivo, son las tres principales aproximaciones seguidas para obtener estimas de la diversidad biológica cuando falta la información biológica (Gaston, 1996). En adelante me centraré en la última de éstas aproximaciones, describiendo sus requerimientos y algunos fundamentos básicos sobre el Análisis de Regresión , la técnica estadística generalmente aplicada en esta metodología. Después repasaré los principales inconvenientes a tener en cuenta, enumerando algunas soluciones que pueden ser de utilidad a la hora de encontrar funciones predictivas de mayor capacidad. Ejemplos de esta metodología e información más detallada pueden encontrarse en Austin et al. (1984 y 1996), Buckland & Elston (1993), Heikkinen & Neuvonen (1997), Kirkpatrick & Brown (1994), Nicholls (1989) o Margules et al. (1987).
Son necesarios tres requisitos para buscar una función predictiva:
- i) una serie de unidades espaciales cuyo inventario faunístico sea fiable y bien establecido
- ii) datos ambientales veraces para cada una de esas unidades
- iii) una metodología capaz de generar una ecuación con las variables explicativas que permita predecir la variable dependiente (número de especies o presencia-ausencia en el caso de una única especie).
Ya hemos comentado el problema del esfuerzo de muestreo. Respecto al segundo requisito, para reunir información ambiental de calidad suele ser necesario un esfuerzo considerable debido, generalmente, a la falta de fuentes y a su dispersión. Los mapas temáticos constituyen una posibilidad adecuada siempre y cuando nuestra escala espacial de análisis no sea muy detallada y los datos de la variable cartografiada no estén obsoletos. Para superponer la cartografía ambiental y la topográfica, de modo que pueda calcularse el valor promedio de la variable en la unidad espacial que deseamos, es fundamental la utilización de los Sistemas de Información Geográfica
(SIGs). Un SIG es un tipo especializado de base de datos capaz de manejar datos geográficos como imágenes o mapas de la misma porción del territorio, de modo que es posible superponer y analizar las características espaciales y temáticas de una zona concreta
(Miller, 1994; ver
http://www.geo4gis.com/esri.htm ó
http://www.clarklabs.org/).
Respecto a las variables a utilizar, numerosos estudios han tratado de poner de manifiesto la relación existente entre el número de especies de un grupo determinado y distintos parámetros ambientales (ver Gaston, 1996 y referencias allí citadas). Estos trabajos demuestran que el número de variables ambientales que pueden utilizarse para buscar una función predictiva es muy grande, siendo difícil decidir cuales son las más convenientes en cada caso concreto. Como criterio preliminar, parece conveniente seleccionar aquellas variables relacionadas con la energía que entra en el sistema como productividad, evapotranspiración, pluviosidad, temperatura, etc. (ver Wright et al., 1993), pero la amplitud altitudinal o alguna medida de la heterogeneidad ambiental suelen dar también buenos resultados (Wohlgemuth, 1998). Finalmente, si sospechamos que la influencia de la alteración antrópica del territorio puede ser una variable importante, resulta útil considerar alguna medida del uso del suelo o del tipo de paisaje.
Existen diversos métodos, unos más sofisticados que otros, para intentar predecir el número de especies o la presencia de una sola de ellas a partir de variables ambientales. Por ejemplo, los algoritmos genéticos (Mitchell, 1991; ver http://kaos.erin.gov.au/general/biodiv_model/ERIN/GARP/home.html), el análisis de huecos (Gap Analysis, Scott et al., 1993; ver http://www.sdvc.uwyo.edu/wbn/gap.html), los autómatas celulares (Carey, 1996) o los métodos de clasificación y regresión (Regression Tree Analysis; Iverson & Prasad, 1998). Sin embargo, el método más socorrido y sencillo para explorar la relación entre los datos de especies y diversas variables es el Análisis de Regresión (Ter Braak & Looman, 1995).
Si se poseen datos de varias variables ambientales explicativas deben utilizarse los Análisis de Regresión múltiples que, en esencia, siguen los mismos principios que los Análisis de Regresión simples. En estos análisis suele ser frecuente que algunas variables independientes estén correlacionadas entre ellas, por lo que hay que conducirse cuidadosamente para realizar la elección de las variables significativas. Puede hacerse un Análisis de Regresión Múltiple con todas las variables a la vez y comprobar cuales tienen una pendiente significativamente diferente de cero, pero también pueden eliminarse aquellas variables no significativas mediante un proceso de eliminación hacia delante (forward) o hacia atrás (backward). En el primero se realiza una regresión individual sobre cada una de las variables independientes y se elige aquella que explica un mayor porcentaje de la variación en la variable dependiente. Entonces se vuelven a realizar regresiones parciales incluyendo la variable elegida y, una a una, se introduce el resto de las variables hasta encontrar aquella que explica un mayor porcentaje de la varianza que queda aún por explicar. El proceso finaliza cuando no puede encontrarse ninguna otra variable que contribuya significativamente. En el procedimiento de selección backward se comienza por incluir todas las variables a la vez, eliminándose en cada paso la variable explicativa menos significativa, hasta que sólo queden aquellas que contribuyen significativamente a explicar la variación de la variable dependiente. Un método más fiable es el Análisis de Regresión por Pasos (Stepwise Multiple Regression) en el cual se alterna un proceso de selección forward de las variables con una eliminación backward, de modo que cada vez que se incluye una nueva variable en el modelo, se comprueba la significación de todas las previamente incluidas. Desgraciadamente puede ocurrir que los distintos métodos elijan diferentes conjuntos de variables.
Los Análisis de Regresión por Pasos son cada vez más frecuentemente criticados (ver, por ejemplo, http://www.fmdc.calpoly.edu/libarts/jgill/360.stepwise.html), debido a que, con relativa frecuencia, son incapaces de producir una función en la cual las variables integrantes sean las de mayor poder predictivo. En general, los mayores inconvenientes se producen cuando existe un alto número de variables explicativas y cuando algunas de éstas están correlacionadas entre sí. En esos casos, el grado de correlación entre la variables predictivas, suele afectar la frecuencia con que aparecen aquellas que son verdaderamente explicativas, pudiendo entrar a formar parte del modelo variables que no poseen ninguna significación biológica o estén pobremente relacionadas con la variable dependiente. Si tenemos N variables independientes, existen 2N posibles ecuaciones y varias de ellas pueden ser capaces de representar los datos igualmente bien (Daniel & Wood, 1980). ¿Cuál debemos elegir? La solución óptima consiste en estudiar todas las ecuaciones posibles y elegir la que posee menores residuos. Esta aproximación, aunque infalible, puede ser inviable en la práctica con los métodos tradicionales: si poseemos 15 variables independientes, existen 32.728 ecuaciones diferentes. Cuando se trata únicamente de buscar una función que nos permita predecir no es trascendente que la función obtenida excluya variables significativas o incluya otras menos explicativas y difíciles de interpretar biológicamente. Podemos identificar los factores correlacionados con la diversidad de especies de un grupo cualquiera a una determinada escala espacial, pero resulta más difícil decidir si esa correlación es accidental o si puede identificarse una causa biológica subyacente (Shipley, 1999).
3. 2. - Los inoportunos inconvenientes
La búsqueda de una relación sencilla que pueda ofrecernos una función de alto valor predictivo es, con toda seguridad, una pretensión exagerada e irreal. Estimar el número de especies (o la presencia de una sola de ellas) en un territorio concreto y a una escala espacial determinada, mediante la utilización de variables ambientales, es una aproximación más simple que colectar, identificar y contar directamente el número de especies, pero no está exenta de dificultades, a continuación, examinaré las que considero fundamentales.
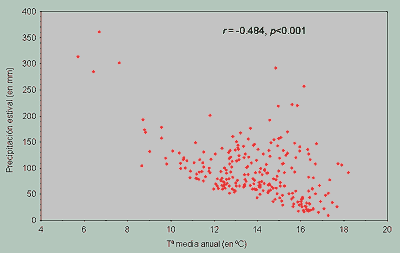
Como se mencionó anteriormente, un problema frecuente es la correlación existente entre las distintas variables ambientales que se utilizan (Figura 3), un atributo propio de los sistemas que, como la Biosfera, poseen una notable complejidad en las relaciones entre sus elementos. Muchas variables ambientales varían de forma similar a lo largo de un gradiente espacial, de modo que se pierde la necesaria independencia entre sus valores. Elegir una variable explicativa suele suponer desestimar otras relacionadas con ella, pero que son ligeramente menos efectivas a la hora de predecir la variable dependiente.
|
|
|
Figura 3.- Relación entre la temperatura media anual en las 255 cuadrículas UTM de 50 km de la Península Ibérica y la precipitación estival, un ejemplo de dos variables que no son independientes ya que una temperatura ambiental mayor suele asociarse con una sequía estival más pronunciada. En la figura se indica el coeficiente de correlación de Pearson entre las dos variables. |
Por ello, pueden encontrarse distintas funciones con similar capacidad predictiva constituidas por conjuntos de variables ambientales diferentes. Cualquiera de esas funciones puede ser útil a la hora de realizar pronósticos, pero siempre hay que tener cuidado con las interpretaciones causales, es decir, con la consideración de esas variables como los factores que originan la modificación en la variable estudiada. Examinar previamente el grado de correlación existente entre las variables explicativas no soluciona completamente el problema, pero permite desechar algunas variables ambientales y conocer las razones de su elección o rechazo. Una alternativa consiste en utilizar algún método multivariante de ordenación, como el análisis de componentes principales (ver Legendre & Legendre, 1998). Con estos métodos puede reducirse el número de variables mediante la generación de otras nuevas que son composiciones de las anteriores y, lo que es más importante, que no están correlacionadas entre sí. El inconveniente es que, en no pocas ocasiones, es difícil interpretar estas nuevas variables.
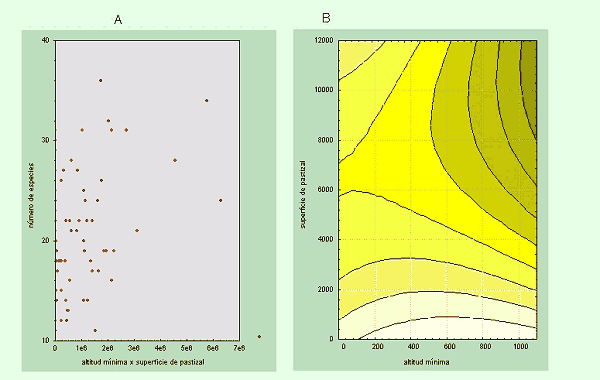
Otro inconveniente habitual es que, a veces, el efecto de una variable depende del valor de otra y esa interacción posee un mayor valor predictivo que las propias variables por separado (Figura 4) (ver Margules et al. 1987).
|
|
|
Figura 4.-Relación entre el número de especies de Escarabeidos y la interacción entre altitud mínima y la superfice de pastizal (A). Como puede verse en el gráfico de contorno (B), las localidades con una altitud mínima muy baja o con poca superficie de pastizal albergan pocas especies (zonas amarillas), como también ocurre en las localidades con una gran superficie de pastizales y altitudes bajas o en las localidades con altitudes mínimas elevadas pero poca superficie de pastizal. Sin embargo, cuando el valor de ambas variables es grande su efecto sinérgico produce un aumento notable de la riqueza de especies. Lo que en realidad demuestra esta interacción es que los pastizales de las zonas montañosas ibéricas son especialmente ricos en especies de escarabeidos. |
Para comprobar si las interacciones son efectivas a la hora de predecir la variable dependiente, se utiliza el producto de dos variables (x3=x1 * x2) como una variable más, comprobándose su capacidad predictiva mediante su inclusión en el Análisis de Regresión. Un tipo de interacciones especialmente interesantes, son aquellas que existen entre una variable espacial (latitud, longitud o algún término cuadrático o cúbico de éstas) y una variable ambiental. En el caso hipotético de que una variable de interacción de este tipo posea valor predictivo, es probable que la variable ambiental en cuestión tenga un efecto significativo únicamente en determinadas porciones del territorio.
La relación entre las variables ambientales y la variable dependiente no tiene por qué ser lineal (Figura 5) (ver Austin et al., 1996).
|
|
|
Figura 5.- Relación entre el número de especies de Escarabedios en la Península Ibérica y la temperatura media mínima en cuadrículas UTM de 50 km, como puede verse la relación es parabólica (Y= c + b1X + b2 X2) ya que esta función explica más y mejor la variación del número de especies (R2 =12.9%) que una función linear (R2 = 1.7%). La relación significa que cuando la temperatura mínima es muy baja o muy alta el número de especies es mayor y que los menores valores de riqueza se dan a niveles de temperatura intermedios. |
Es más, hay numerosos ejemplos de relaciones que no son lineares. Tal es el caso de las que se dan entre productividad y diversidad (Rosenzweig & Abramsky, 1993) o entre diversidad y altitud (McCoy, 1990): parabólicas, exponenciales, potenciales, etc. Las relaciones deben de ser lineales para la mayoría de los métodos de regresión y estadísticos sencillos. Por ello, es conveniente visualizar una a una las relaciones entre las variables explicativas y la variable dependiente y en el caso de que no sean lineares intentar linearizarlas mediante algún tipo de transformación.
Como generalmente las variables biológicas no se distribuyen siguiendo la curva Normal, ni las relaciones entre ellas suelen lineales, se está imponiendo cada vez con mayor frecuencia el uso de los Modelos Lineales Generalizados (McCullagh & Nelder, 1983; Crawley, 1993). La utilización de esta técnica estadística constituye una herramienta fundamental para solventar los inconvenientes anteriores, ya que permite especificar el tipo de distribución para los errores y elaborar modelos aunque las relaciones entre las variables no sean lineales. Además, facilita el análisis de las interacciones, siendo utilizable, asimismo, en el caso de variables categóricas (ver algunos ejemplos en Austin et al., 1996 o Heikkinen & Neuvonen, 1997).
Las variables ambientales están a menudo espacialmente autocorrelacionadas, o sea, el valor de la variable en una localidad depende del valor en las localidades contiguas, violándose así la independencia entre las observaciones requerida por la mayoría de las pruebas estadísticas (Cliff & Ord, 1981; Odland, 1988). La autocorrelación de una variable puede suprimirse con bastante efectividad mediante un Trend Surface Analysis (TSA; ver Legendre, 1993). Se trata de construir un polinomio de tercer grado con la latitud (LAT) y la longitud (LON) de cada observación (LAT + LON + LAT2 + LAT x LON + LON2 + LAT3 + LAT2 x LON + LAT x LON2 + LON3) y someter sus nueve términos como variables independientes a un análisis de regresión por pasos, con la variable a la cual queremos quitar su estructura espacial como dependiente. De este modo, si aparece algún término significativo, la variable posee una estructura espacial y pueden elegirse los residuos de la regresión (la parte de la variable no explicada por el espacio), como una estima de la variable sin autocorrelación o estructura espacial. Como casi todas las variables ambientales varían siguiendo algún gradiente espacial, sobre todo a escala geográfica, eliminar el componente espacial de una variable supone casi siempre desechar una parte importante de su capacidad explicativa. De este modo, es necesario:
Como casi todas las variables ambientales varían siguiendo algún gradiente espacial, sobre todo a escala geográfica, eliminar el componente espacial de una variable supone casi siempre desechar una parte importante de su capacidad explicativa. De este modo, es necesario:- i) comprobar que las variables que utilizamos están autocorrelacionadas
- ii) incorporar sin problema esa autocorrelación en nuestros modelos predictivos
- iii) examinar los residuos del modelo para ver si estos están autocorrelacionados (Cliff & Ord, 1981; Legendre & Legendre, 1998; Smith, 1994).
Si los residuos (lo que no predice nuestro modelo) poseen una clara estructura espacial o están autocorrelacionados, es que probablemente no hemos considerado alguna variable con una clara variación espacial. Será entonces necesario buscar esa variable o variables (elaborar un mapa de esos residuos puede dar algunas pistas) e introducirla para lograr que la capacidad predictiva de nuestro modelo no sea significativamente mayor en unos lugares determinados que en otros. Una manera de asegurar que la variación espacial de nuestra variable dependiente esté recogida, disminuyendo de este modo las posibilidades de que aparezcan residuos autocorrelacionados, es introducir al final del modelo y como variables independientes, los nueve términos del polinomio de tercer grado de la latitud y la longitud. Para realizar los análisis de autocorrelación existen algunos programas informáticos de acceso gratuito:
R-Package, http://www.fas.umontreal.ca/biol/casgrain/en/labo/R/index.html RookCase, http://aix1.uottawa.ca/academic/arts/geographie/lpcweb/sections1/software/frmsoft.htm)
Utilizando el número de registros contenidos en una exhaustiva base de datos sobre los Scarabaeidae Ibéricos como medida de esfuerzo, hemos predicho la distribución geográfica de la riqueza de especies en la Península Ibérica, mediante la utilización de variables ambientales. En primer lugar, se evaluó el esfuerzo de muestreo en toda la península a escala de cuadrículas UTM de 50 km. Para ello, se definieron primeramente las regiones fisiográficas del territorio peninsular utilizando variables climáticas (temperatura media anual, variación de la temperatura anual, días de sol al año, precipitación total anual, variación de la precipitación estival y anual) y topográficas (altitud media y rango altitudinal). A continuación, se analizó el esfuerzo de muestreo diferencial entre áreas, investigando la relación asintótica del número de especies registradas a diferentes niveles de esfuerzo de muestreo. Posteriormente, se estableció el grupo de cuadrículas UTM bien muestreadas en cada una de las subregiones, mediante una jerarquía de esfuerzos de muestreo subjetivamente definidos a diferentes tasas de incremento del número de especies. Se identificaron un total de 82 cuadrículas (32.2%) adecuadamente muestreadas (Figura 1). Como variables explicativas se utilizaron los valores de 24 variables en esas 82 cuadrículas (Tabla 1): dos espaciales, dos geográficas, cuatro topográficas, tres geológicas, ocho climáticas y cinco relativas a usos del suelo, más los correspondientes términos de interacción entre las diferentes variables ambientales (n=231) y entre éstas y las espaciales (n=44).
Tabla 1. - Variables explicativas utilizadas para elaborar un modelo predictivo de la distribución del número de especies de Escarabeidos en la Península Ibérica. Los datos de cada variables se tomaron para cada cuadrícula UTM de 50 km utilizando un modelo digital del terreno, mapas de usos del suelo y mapas climáticos. Para obtener los datos promedios en cada cuadrícula, dicha cartografía se superpuso con un mapa digital de las cuadrículas mediante un Sistema de Información Geográfica. La diversidad de usos del suelo y la diversidad geológica se calcularon mediante el índice de diversidad de Shannon utilizando los valores de todas las categorías de usos del suelo (n=44) y geológicas (n=3). Mediante Modelos Lineares Generalizados se averiguó la significación de las funciones lineales (y=c+bx), cuadráticas (y=c+bx+bx2) o cúbicas (y=c+bx+bx2+bx3) de cada variable a la hora de explicar el número de especies en las 82 cuadrículas UTM bien muestreadas, mostrándose la función elegida en cada caso.
|
Variables |
Función seleccionada |
|
Espaciales |
|
|
Latitud |
Cúbica |
|
Longitud |
Linear |
|
Geográficas |
|
|
Superficie terrestre en cada cuadrícula |
Linear |
|
Distancia a los Pirineos |
Linear |
|
Topográficas |
|
|
Altitud mínima |
Linear |
|
Altitud máxima |
Linear |
|
Altitud media |
Linear |
|
Diferencia de altitudes |
Linear |
|
Geológicas |
|
|
Superficie caliza |
Linear |
|
Superficie silícea |
Linear |
|
Diversidad geológica |
Linear |
|
Climáticas |
|
|
Temperatura media de las mínimas |
Cuadrática |
|
Temperatura media de las máximas |
Linear |
|
Temperatura media anual |
Cuadrática |
|
Variación anual de temperatura |
Linear |
|
Precipitación anual |
Cúbica |
|
Precipitación estival |
Linear |
|
Variación anual de precipitaciones |
Linear |
|
Días con sol anuales |
Linear |
|
Usos del suelo |
|
|
Superficie cultivada y urbana |
Linear |
|
Superficie forestal |
Linear |
|
Superficie con matorral |
Linear |
|
Superficie con pastizal |
Cúbica |
|
Diversidad de usos del suelo |
Cúbica |
Para elegir el modelo predictivo se examinó primeramente la significación de cada una de las variables ambientales, comprobando si su relación con el número de especies era una función lineal (y = x), cuadrática (y = x+x2) o cúbica (y = x + x2 + x3). La función de la variable ambiental con una mayor capacidad explicativa ingresó en primer lugar en un análisis de regresión por pasos. Una vez incluida esa primera variable, se introdujeron secuencialmente cada una de las restantes variables, eligiendo aquella que mejoraba más el modelo. Una vez incluidas todas las variables ambientales significativas, se examinaron todos los posibles pares de interacciones entre variables. Cada interacción era añadida al modelo hasta entonces resultante y una vez elegida la interacción más significativa, el proceso se repetía hasta que no se encontraba ninguna otra interacción significativa. Por último se añadieron los nueve términos del polinomio de tercer grado de la latitud y la longitud. Tras cada inclusión de una variable significativa (forward), se comprobó si cualquiera de las anteriormente introducidas dejaba de ser significativa (backward).
La elaboración completa de un primer modelo final permitió comprobar que algunas cuadrículas poseían valores reales muy superiores a los que predecía la función, mientras que otras poseían valores reales inferiores a los predichos ('outliers'). Se trataba de cuatro cuadrículas ubicadas en los alrededores de Madrid y Barcelona con una gran cantidad de información faunística acumulada y de las tres cuadrículas ubicadas en las Islas Baleares. Ya que utilizar el número de especies observado en estas cuadrículas para predecir la riqueza del resto, podría producir resultados erróneos, se elaboró un nuevo modelo tras eliminar estas 7 cuadrículas.
El modelo final permite explicar el 62.4% de la varianza en el número de especies y contiene ocho variables (Tabla 2): altitud máxima, el término cuadrático de la superficie de pastizal, la diversidad de usos del suelo, las interacciones superficie forestal x diversidad geológica, área terrestre x altitud máxima, superficie caliza x diversidad geológica y los términos cuadrático y cúbico de la latitud. Un examen de los residuos del modelo mostró la ausencia de características aberrantes y autocorrelacion.
Tabla 2.- Resultados del análisis de regresión múltiple por pasos entre el número de especies de Escarabaeidos en las cuadrículas Ibéricas bien muestreadas (Figura 1) y las variables ambientales y espaciales elegidas (Tabla 1). Se muestran las variables significativas, sus coeficientes y el error en la estima de los mismos.
|
Variables |
Coeficientes |
Error Estándar |
|
Altitud máxima |
0.062 |
0.026 |
|
+ Superficie de pastizal2 |
0.014 |
0.006 |
|
+Diversidad de usos del suelo |
0.114 |
0.041 |
|
+Superficie forestal x Diversidad geológica |
-0.079 |
0.025 |
|
+Altitud máxima x Area terrestre |
0.093 |
0.026 |
|
+Superficie caliza x Diversidad geológica |
0.054 |
0.029 |
|
+ Latitud2 |
-0.021 |
0.009 |
|
+ Latitud3 |
-0.009 |
0.002 |
|
intercepto |
2.940 |
0.050 |
Aplicando la función predictiva al resto de las cuadrículas ibéricas obtuvimos la distribución del número de especies que se refleja en la Figura 5. Finalmente validamos nuestro modelo elaborando 75 funciones predictivas (una por cada observación) en las que los parámetros de cada ecuación se estimaban utilizando sólo los datos de 74 cuadrículas y la función resultante se aplicaba sobre la cuadrícula excluida (Figura 6).
|
|
|
Figura 6.- Mapa de distribución del número de especies de Escarabeidos en la Península Ibérica de acuerdo con el modelo predictivo final (Tabla 2). El mapa ha sido elaborado mediante interpolación utilizando los datos anteriores. El color amarillo marca el límite de las 20 especies por cuadricula UTM de 50 km. |
4.- Los factores históricos y el espacio
Las funciones predictivas resultantes producen un mapa de distribución potencial, un mapa que refleja el área con las condiciones ambientales "convenientes" para que se presente esa especie o esa riqueza de especies. Sin embargo, una de las observaciones que alimentan el estudio biogeográfico es que siempre hay un lugar que parece idóneo ambientalmente para una especie, pero que no está habitado por ella (por ejemplo, cada región mediterránea tiene riquezas y especies distintas; Ver Ricklefs & Schluter, 1993). Cuanto mayor es la escala espacial de análisis, más frecuente es este fenómeno debido, lógicamente, a la actuación de factores de carácter único e irrepetible que condicionan la distribución. Se trata de la historia evolutiva propia de cada grupo, de la historia y los avatares propios de cada región y de las características geográficas de la misma. Evidentemente, la importancia de los factores ambientales a la hora de restringir la distribución de las especies es limitada, de modo que elaborar funciones predictivas que únicamente tengan en consideración variables ambientales producirá, generalmente, modelos incompletos. Ello será especialmente cierto cuando la escala espacial de análisis sea amplia, como exige el estudio geográfico de la variación del número de especies. Historia y geografía también juegan y es necesario incluirlas ¿Cómo podemos hacerlo?
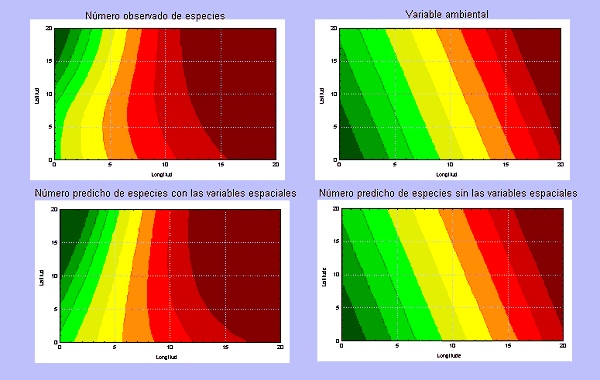
Si los factores históricos y geográficos ejercen una manifiesta influencia sobre la distribución de las especies y si el efecto de estos factores tiene una expresión espacial, la inclusión de funciones complejas de la latitud y la longitud, puede mejorar la capacidad de predicción de las funciones obtenidas. Veamos un ejemplo. En la Figura 7 se muestra la distribución hipotética de una variable ambiental que decrece en sus valores hacia el sur y hacia el oeste y, a la vez, una distribución hipotética de la riqueza en especies de un taxon que es función de dicha variable ambiental (el número de especies es la raíz cuadrada del valor de la variable ambiental). Supongamos que por causas históricas o geográficas no asociadas a factores ambientales, el número de especies disminuye en el cuadrante noroccidental sombreado (Figura 7A). En este caso, elaborar una función predictiva mediante un análisis de regresión, utilizando sólo la variable ambiental permite explicar el 74,6% de la variación en el número de especies. Sin embargo, si se incluye esa misma variable ambiental junto a los 9 términos del polinomio de tercer grado de la latitud y la longitud, la función predictiva permite explicar el 92,1% de la variación en el número de especies (ver Figura 7). La longitud y la interacción entre la latitud y la longitud2 resultan ser los términos espaciales que mejoran la capacidad explicativa del modelo.
| A | B | ||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 1 | 2 | 4 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 | 88 | 92 | 96 | 100 | ||
| 0 | 0 | 0 | 1 | 2 | 4 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 23 | 27 | 31 | 35 | 39 | 43 | 47 | 51 | 55 | 59 | 63 | 67 | 71 | 75 | 79 | 83 | 87 | 91 | 95 | 99 | ||
| 0 | 0 | 0 | 1 | 2 | 4 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 10 | 10 | 22 | 26 | 30 | 34 | 38 | 42 | 46 | 50 | 54 | 58 | 62 | 66 | 70 | 74 | 78 | 82 | 86 | 90 | 94 | 98 | ||
| 0 | 0 | 0 | 1 | 3 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 10 | 10 | 21 | 25 | 29 | 33 | 37 | 41 | 45 | 49 | 53 | 57 | 61 | 65 | 69 | 73 | 77 | 81 | 85 | 89 | 93 | 97 | ||
| 0 | 0 | 0 | 1 | 3 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 10 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 | 88 | 92 | 96 | ||
| 0 | 0 | 0 | 1 | 3 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 10 | 19 | 23 | 27 | 31 | 35 | 39 | 43 | 47 | 51 | 55 | 59 | 63 | 67 | 71 | 75 | 79 | 83 | 87 | 91 | 95 | ||
| 0 | 0 | 1 | 1 | 3 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 10 | 18 | 22 | 26 | 30 | 34 | 38 | 42 | 46 | 50 | 54 | 58 | 62 | 66 | 70 | 74 | 78 | 82 | 86 | 90 | 94 | ||
| 0 | 0 | 1 | 1 | 3 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 10 | 17 | 21 | 25 | 29 | 33 | 37 | 41 | 45 | 49 | 53 | 57 | 61 | 65 | 69 | 73 | 77 | 81 | 85 | 89 | 93 | ||
| 0 | 1 | 2 | 2 | 3 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 | 88 | 92 | ||
| 1 | 2 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 15 | 19 | 23 | 27 | 31 | 35 | 39 | 43 | 47 | 51 | 55 | 59 | 63 | 67 | 71 | 75 | 79 | 83 | 87 | 91 | ||
| 1 | 3 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 14 | 18 | 22 | 26 | 30 | 34 | 38 | 42 | 46 | 50 | 54 | 58 | 62 | 66 | 70 | 74 | 78 | 82 | 86 | 90 | ||
| 2 | 3 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 13 | 17 | 21 | 25 | 29 | 33 | 37 | 41 | 45 | 49 | 53 | 57 | 61 | 65 | 69 | 73 | 77 | 81 | 85 | 89 | ||
| 3 | 4 | 4 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 | 88 | ||
| 3 | 4 | 4 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 11 | 15 | 19 | 23 | 27 | 31 | 35 | 39 | 43 | 47 | 51 | 55 | 59 | 63 | 67 | 71 | 75 | 79 | 83 | 87 | ||
| 3 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 14 | 18 | 22 | 26 | 30 | 34 | 38 | 42 | 46 | 50 | 54 | 58 | 62 | 66 | 70 | 74 | 78 | 82 | 86 | ||
| 3 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 13 | 17 | 21 | 25 | 29 | 33 | 37 | 41 | 45 | 49 | 53 | 57 | 61 | 65 | 69 | 73 | 77 | 81 | 85 | ||
| 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 | ||
| 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 7 | 11 | 15 | 19 | 23 | 27 | 31 | 35 | 39 | 43 | 47 | 51 | 55 | 59 | 63 | 67 | 71 | 75 | 79 | 83 | ||
| 2 | 3 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 6 | 10 | 14 | 18 | 22 | 26 | 30 | 34 | 38 | 42 | 46 | 50 | 54 | 58 | 62 | 66 | 70 | 74 | 78 | 82 | ||
| 2 | 3 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 5 | 9 | 13 | 17 | 21 | 25 | 29 | 33 | 37 | 41 | 45 | 49 | 53 | 57 | 61 | 65 | 69 | 73 | 77 | 81 |
|
|
|
Figura 7.- Arriba, distribución hipotética del número de especies (A). Dicho número decrece de manera similar a como lo hace la variable ambiental, cuyos valores se muestran en la matriz de la derecha. En realidad, el número de especies es la raíz cuadrada de la variable ambiental, excepto en las 54 cuadrículas en rojo del cuadrante noroccidental, en las que la tendencia decreciente es mucho más acusada. (B) Variación de una variable ambiental hipotética que disminuye geométricamente una unidad de norte a sur y dos unidades de este a oeste. Los cuatro gráficos de contorno expuestos reflejan la distribución del número de especies y de la variable ambiental (parte superior) y la distribución predicha según dos funciones diferentes: una que incorpora únicamente la información ambiental (parte inferior derecha) y otra que incorpora la información ambiental y espacial parte inferior izquierda. La gama de colores corresponde a incrementos del número de especies del verde al rojo. |
Los factores de carácter único e irrepetible pueden ejercer una profunda influencia sobre la diversidad biológica, sobre todo en aquellos territorios en los que existe una yuxtaposición de táxones con distintas historias evolutivas. Incorporar la componente espacial en estos casos, puede permitir elaborar funciones predictivas más fiables y competentes ya que, generalmente, el efecto de estos factores suele estar delimitado geográficamente. Sin embargo, en el caso de que el espacio posea una alta capacidad explicativa, no se debe atribuir ésta únicamente a factores de tipo histórico o geográfico. En la práctica, resulta difícil discernir si la capacidad explicativa del espacio se debe a factores de este tipo o a alguna otra variable ambiental no considerada (ver Legendre, 1990 y Borcard et al., 1992). Sin embargo, si utilizando diversos tipos de variables ambientales, el espacio todavía posee una apreciable capacidad explicativa es licito sospechar que ésta se deba a factores histórico-geográficos.
Conocer la distribución geográfica del número de especies de un grupo taxonómico cualquiera es una tarea prácticamente inabordable a corto plazo, incluso en aquellos países con una dilatada tradición taxonómica. Esto es especialmente cierto cuando tratamos con algún grupo de insectos y con escalas espaciales geográficas. Ante esta situación, una estrategia recomendable consiste en recopilar la información taxonómica y corológica dispersa en las colecciones y la bibliografía, con el fin de delimitar los territorios insuficientemente muestreados y aquellos en los que el inventario faunístico puede considerarse bien establecido. Cuando, como resultado de este análisis, la información sobre la distribución de las especies es insuficiente, deberá incrementarse el esfuerzo de inventario pero, en este caso, tendremos una valiosa información sobre la ubicación de las zonas a prospectar y sobre el esfuerzo suplementario a realizar. Si, por el contrario, la información biológica es suficiente, pueden aplicarse distintas aproximaciones metodológicas que, dentro de unos límites razonables, son capaces de proporcionar una estima de la diversidad existente en cada unidad espacial analizada, mediante la utilización de diversas variables ambientales. La distribución de la diversidad generada mediante este proceso debe considerarse una primera aproximación. Aproximación que puede y debe validarse y mejorarse paulatinamente mediante la realización de posteriores colectas en distintos territorios.
- Ahlberg, P.E., Clack, J.F. & Luksevics, E. 1996. Rapid braincase evolution between Panderichthys and the earliest tetrapods. Nature 381: 61-64.
- Austin, M.p., Cunningham, R.B. & Fleming, P.M. 1984. New approaches to direct gradient analysis using environmental scalars and statistical curve-fitting procedures. Vegetatio 55: 11-27.
- Austin, M.P., Pausas, J.G. & Nicholls, A.O. 1996. Patterns of tree species richness in relation to environment in south-eastern New South Wales, Australia. Australian Journal of Ecology 21: 154-164.
- Avers, C.J. 1989. Process and Pattern in Evolution. Oxford University Press, New York.
- Baraud, J. 1992. Coléoptères Scarabaeoidea d'Europe. Fédération française des Sociétés de Sciences Naturelles et Société Linnéenne de Lyon, Lyon.
- Beaufort, F. De & Maurin, H. 1988. Le Secrétariat de la Faune et de la Flore et l'inventaire du patrimoine naturel: objetifs, méthodes et fonctionnement. Secrétariat Faune-flore/MNHN, París.
- Baltanás, A. 1992. On the use of some methods for the estimation of species richness. Oikos 65:484-492.
- Beerling, D.J. & Woodward, F.I. 1996. Palaeo-ecological perspectives on plant responses to global change. Trends in Ecology and Evolution 11: 20-23.
- Blondel, J. 1995. Biogeographie. Approche écologique et évolutive. Masson, Paris.
- Borcard, D., Legendre, P. & Drapeau, P. 1992. Partialling out the spatial component of ecological variation. Ecology 73: 1045-1055.
- Buckland, S.T. & Elston, D.A. 1993. Empirical models for the spatial distribution of wildlife. Journal of Applied Ecology 30: 478-495.
- Carey, P.D. 1996. A cellular automaton for predicting the distribution of species in a changed climate. Global Ecology and Biogeography Letters 5: 217-226.
- Chao, A. & Lee, S.M. 1992. Estimating the number of classes via sample coverage. Journal of American Statistics Assocciation 87: 210-217.
- Chazdon, R. L., Colwell, R. K., Denslow, J. S. &. Guariguata, M.R. 1998. Statistical methods for estimating species richness of woody regeneration in primary and secondary rain forests of northeastern Costa Rica.. En F. Dallmeier & J. A. Comiskey (eds.), págs. 285-309. Forest biodiversity research, monitoring and modeling: Conceptual background and Old World case studies. Parthenon Publishing, Paris.
- Cliff, A.D. & Ord, J.K. 1981. Spatial Processes.: Models and Applications. Pion, London.
- Colwell, R. K. 1997. EstimateS. Statistical estimation of species richness and shared species from samples. Version 5. User's guide and application published at http://viceroy.eeb.uconn.edu/estimates.
- Colwell, R. K. & Coddington, J.A. 1995. Estimating terrestrial biodiversity through extrapolation. En Hawksworth, D. L. (ed.), págs. 101-118. Biodiversity, Measurement and Estimation. Chapman & Hall, London.
- Coope, G.R. 1979. Late Cenozoic fossil Coleoptera: Evolution, biogeography and ecology. Annual Reviews of Ecology and Systematics 10: 247-267.
- Crawley, M.J. 1993. GLIM for Ecologists. Blackwell Science Ltd., Oxford.
- Daniel, C. & Wood, F.S. 1980. Fitting Equations to Data. John Wiley & Sons, New York.
- Davis, F.W. 1994. Mapping and monitoring terrestrial biodiversity using geographic information systems. En Peng, C.I. & Chou, C.H. (eds.), págs. 461-471. Biodiversity and Terrestrial Ecosystems. Institute of Botany, Academia Sinica Monograph series No 14, Taipei.
- Elias, S.A. 1994. Quaternary Insects and their Environments. Smithsonian Institution Press, Washington.
- Fagan, W.F. & Kareiva, P.M.. 1997. Using compiled species list to make biodiversity comparisons among regions: a test case using Oregon butterflies. Biological Conservation 80: 249-259.
- Farrell, B.D., Mitter, C. & Futuyma, D.J. 1992. Diversification at the insect-plant interface. BioScience 42: 34-42.
- Gaston, K.J. 1996. Species richness: measure and measurement.. En Gaston, K.J. (ed.), págs. 77-113. Biodiversity. A biology of numbers and difference. Blackwell Science Ltd., Oxford.
- Hanski, I. & Cambefort Y. (eds.). 1991. Dung Beetle Ecology, Princeton University Press, New Jersey.
- Harding, P.T. & Sheail, J. 1992. The Biological Records Centre: a pioneer in data gathering and retrieval. En Harding, P.T. (ed.), págs. 5-19. Biological Recording of Changes in British Wildlife . Institute of Terrestrial Ecology, London.
- Heikkinen, R.K. & Neuvonen, S. 1997. Species richness of vascular plants in the subarctic landscape of northern Finland: modelling relationships to the environment. Biodiversity and Conservation 6: 1181-1201.
- Hengeveld, R. 1990. Dynamic Biogeography. Cambridge University Press, Cambridge.
- Hengeveld, R. 1997. Impact of Biogeography on a population-biological paradigm shift. Journal of Biogeography 24: 541-547.
- Hulbert, S.H. 1971. The non-concept of species diversity: A critique and alternative parameters. Ecology 52: 577-586.
- Huntley, B. & Birks, H.J.B. 1983. An Atlas of Past and Present Pollen Maps for Europe: 0-13,000 Years Ago. Cambridge University Press, Cambridge.
- Iverson, L.R. & Prasad, A.M. 1998. Predicting abundance of 80 tree species following climate change in the eastern United States. Ecological Monographs 68: 465-485.
- Kirkpatrick, J.B. & Brown, M.J. 1994. A comparison of direct and environmental domain approaches to planning reservation of forest higher plant communities and species in Tasmania. Conservation Biology 8: 217-224.
- Krebs, C.J. 1989. Ecological Methodology. Harper and Row, New York.
- Latham, R.E. & Ricklefs, R.E. 1993. Continental comparisons of temperate-zone tree species diversity. En R.E. Ricklefs & Schluter, D. (eds.), págs. 294-314. Species Diversity in Ecological Communities. University of Chicago Press, Chicago.
- Legendre, P. 1990. Quantitative methods and biogeographic analysis. En Garbary, D.J. & South, R.R. (eds.), págs. 9-34. Evolutionary Biogeography of the Marine Algae of the North Atlantic. Nato asi series, Vol G 22, Springer-Verlag, Berlin.
- Legendre, L. & Legendre, P. 1983. Numerical Ecology. Elsevier Scientific Publishing, Amsterdam.
- Legendre, P. & Legendre, L. 1998. Numerical Ecology (2ª edición). Elsevier Scientific Publishing, Amsterdam.
- Lobo, J.M. 1999. Individualismo y adaptación Espacial: un nuevo enfoque para explicar la distribución geográfica de las especies. Boletín de la Sociedad Entomológica Aragonesa (en prensa)
- Lobo, J.M. & Deloya, C. 1993. Una predicción acerca de la diversidad de escarabeidos (Coleoptera, Scarabaeidae) en la Reserva de La Biosfera "La Michilia", Durango, México. Boletín de la Sociedad Veracruzana Zoología 3: 57-63.
- Lobo, J.M., Lumaret, J.P. & Jay-Robert, P. 1997. Les atlas faunistiques comme outils d'analyse spatiale de la biodiversité. Annales de la Société Entomologique de France (N.S.) 33: 129-138.
- Lobo, J. M. & Martín-Piera, F. 1991. La creación de un banco de datos zoológico sobre los Scarabaeidae (Coleoptera: Scarabaeoidea) íbero-baleares: una experiencia piloto. Elytron 5:31-38.
- Lubchenco, J., Olson, A.M., Brubaker, L.B., Carpenter, S.B., Holland, M.M., Hubbell, S.P., Levin, S.A., MacMahon, J.A., Matson, P.A., Melillo, J.M., Mooney, H.A., Peterson, C.H., Pulliam, H.R., Real, L.A., Regal, P.J. & Risser, P.G. 1991. The sustainable biosphere initiative: an ecological research agenda. Ecology 72:371-412.
- Ludwig, J.A. & Reynolds, J.F. 1988. Statistical Ecology. John Wiley & Sons, New York.
- Lumaret, J.P. 1990. Atlas des Coleopteres Scarabéides Laparosticti de France. Museum National d'Histoire Naturelle, Secretariat de la Faune et de la Flore, Paris.
- Margules, C.R., Nicholls, A.O. & Austin, M.P. 1987. Diversity of Eucalyptus species predicted by a multi-variable environment gradient. Oecologia 71 229-232.
- Mayr, E. 1963. Animal Species and Evolution. Harvard University Press, Cambridge.
- McCoy, E.D. 1990. The distribution of insects along elevational gradients. Oikos 58: 313-322.
- McCullagh, P. & Nelder, J.A. 1983. Generalized Linear Models. Chapman and Hall, London.
- Magurran, A. E. 1988. Ecological Diversity and its Measurement. Princeton University Press, New Jersey.
- Margules, C.R. & Austin, M.P. 1994. Biological models for monitoring species decline: the construction and use of data bases. Philosophical Transactions of the Royal Society of London, B. 344: 69-75.
- May, R.M., Lawton, J.H. & Stork, N.E. 1995. Assessing extinction rates. En Lawton, J.H. & May, R.M. (eds.), págs. 1-24. Extinction Rates. Oxford University Press, Oxford.
- Miller, R.I. 1994. Mapping the Diversity of Nature. Chapman and Hall, London.
- Mitchell, N.D. 1991. The derivation of climate surfaces for New Zealand, and their application to the bioclimatic analysis of the distribution of kauri (Agathis australis). Journal of the Royal Society of New Zealand 21: 13-24.
- Murphy, D.D. 1990 Conservation biology and scientific method. Conservation Biology 4: 203-204.
- Nicholls, A.O. 1989. How to make biological surveys go further with generalised linear models. Biological Conservation 50: 51-75.
- Noss, R.F. 1991 From endangered species to biodiversity. En Kohl, K (ed), págs. 227-146. Balancing on the Brink of Extinction: The Endangered Species Act and Lessons for the Future. Island Press, Washington.
- Odland, J. 1988. Spatial Autocorrelation. Sage publications, London.
- Osborne, P.E. & Tigar, B.J. 1992. Interpreting bird atlas data using logistic models: an example from Lesotho, Southern Africa. Journal of Applied Ecology 29: 55-62.
- Palmer, M.W. 1990. The estimation of species richness by extrapolation. Ecology 71: 1195-1198.
- Parker, V. 1999. The use of logistic regression in modelling the distributions of bird species in Swaziland. South African Journal of Zoology 34: 39-47.
- Prendergast, J.R., Wood, S.N., Lawton, J.H. & Eversham, B.C. 1993. Correcting for variation in recording effort in analyses of diversity hotspots. Biodiversity Letters 1: 39-53.
- Reid, W.V., Barber ,C. & Miller, K.R. 1992. Global biodiversity strategy: Guidelines for action to save, study and use Earth's biotic wealth sustainably and equitably. World Resources Institute, New York..
- Ricklefs, R.E. & Schluter, D. (eds.). 1993. Species Diversity in Ecological Communities. University of Chicago Press, Chicago.
- Rollo, C.D. 1994. Phenotypes. Chapman & Hall, London.
- Rosenzweig, M.L. & Abramsky, Z. 1993. How are diversity and productivity related?. En Ricklefs, R.E. & Schluter, D. (eds.), págs. 52-65. Species Diversity in Ecological Communities. University of Chicago Press, Chicago.
- Scott, J.M., Davis, F.W., Csuti, B., Noss, R., Butterfield, B., Groves, C., Anderson, H., Caicco, S., D'Erchia, F., Edwards, T.C., Ulliman, J. & Wright, R.G.. 1993. Gap analysis: a geographic approach to protection of biological diversity. Wildlife Monographs 123: 1-41.
- Shipley, B. 1999. Testing causal explanations in organismal biology: causation, correlation and structural equation modelling. Oikos 86: 374-382.
- Slack, J.M.W. 1994. From Egg to Embryo. Cambridge University Press, Cambridge.
- Smith, P.A. 1994. Autocorrelation in logistic regression modelling of species' distributions. Global Ecology and Biogeography Letters 4: 47-61.
- Soberón, M. J. & Llorente, B.J. 1993. The use of species accumulation functions for the prediction of species richness. Conservation Biology 7: 480-488.
- Soule, M.E. 1991. Conservation tactics for a constant crisis. Science 253: 745.
- Systematics Agenda 2000. 1994. Systematics Agenda 2000: Charting the Biosphere. Technical Report. Systematics Agenda 2000, a Consortium of the American Society of Plant Taxonomy, the Society of Systematic Biologists, and the Wili Hennig Society, in cooperation with the Association of Systematics Collections, New York.
- Ter Braak, C.J.F. & Looman, C.W.N. 1995. Regression. En Jongman, R.H.G., Ter Braak, C.J.F. & van Tongeren, O.F.R. (eds.), págs. 29-77. Data Analysis in Community and Landscape Ecology. Cambridge University Press, Cambridge.
- Turner, A. & Paterson, H.E.H. 1991. Species and speciation: evolutionary tempo and mode in the fossil record reconsidered. Geobios 24: 761-769.
- Walker, P.A. 1990. Modelling wildlife distributions using a geographic information system: kangaroos in relation to climate. Journal of Biogeography 17: 279-289.
- Walter, G.H. & H.E.H. Paterson. 1994. The implications of palaeontological evidence for theories of ecological communities and species richness. Australian Journal of Ecology 19: 241-250.
- Webb, T., Bartlein, P.J., Harrison, S.P. & Anderson, K.H. 1993. Vegetation, lake levels, and climate in eastern North America for the past 18,000 years. En Wright, H.E. et al. (eds.), págs. 468-513. Global Climates Since the Last Glacial Maximum. University of Minnesota Press, Minneapolis.
- Williams, P. & Gaston, K.J. 1994. Measuring more 'diversity': Can higher taxon richness predict wholesale species richness?. Biological Conservation 67: 211-217.
- Wilson, E.O. 1988. The current state of biological diversity. En Wilson, E.O. (ed.), págs. 3-18. Biodiversity. National Academy Press, Washington D.C.
- Wohlgemuth, T. 1998. Modelling floristic species richness on a regional scale: a case study in Switzerland. Biodiversity and Conservation 7: 159-177
- Wright, D.H., Currie, D.J. & Maurer, B.A. 1993. Energy supply and patterns of species richness on local and regional scales. En Ricklefs, R.E. & Schluter, D. (eds.), págs. 66-74. Species Diversity in Ecological Communities: Historical and Geographical Perspectives. Chicago University Press, Chicago.
JORGE M.
LOBO
Departamento de Biodiversidad y Biología Evolutiva
Museo Nacional de Ciencias Naturales, CSIC.
c/ José Gutiérrez Abascal, 2. 28006. Madrid. España
Tfno.: 91 411 13 28
Correo electrónico: mcnj117@mncn.csic.es