Aracnet 7 -Bol. S.E.A., nº 28 (2001) : 147—150.
 Entomología Aplicada
(III)
Entomología Aplicada
(III)
Modelización de la tasa de desarrollo de insectos en función de la temperatura. Aplicación al Manejo Integrado de Plagas mediante el método de grados-día
Vicente Marco
Departamento de Agricultura y Alimentación. Universidad de La Rioja. C/ Madre de Dios, 51. 26006-Logroño. La Rioja.
vicente-santiago.marco@daa.unirioja.es
Resumen: Se hace un análisis del por qué el método de Grados-día es válido para la predicción del desarrollo de los insectos. Para que dicha predicción no sea errónea, es necesario establecer un modelo válido de la correlación entre temperatura y tasa de desarrollo. Se hace un repaso de los diferentes modelos tanto empíricos como biofísicos propuestos por diferentes autores a lo largo del tiempo. Mediante un modelo válido, se puede obtener el umbral mínimo de desarrollo y la integral térmica para cada estado (y, en su caso, estadio) de cada población de insectos estudiada. Con estos datos, se puede aplicar el método de Grados-día en el Manejo Integrado de Plagas para la correcta toma de varias de las decisiones que requiere. Finalmente, se indican una serie de recomendaciones para una correcta utilización del método, así como para poner de manifiesto algunas limitaciones que presenta.
Introducción
Al igual que otros organismos vivos, los insectos son capaces de sobrevivir únicamente dentro de ciertos límites marcados por factores ambientales como la temperatura, la humedad relativa o el fotoperiodo. Dentro de este rango, estos factores influyen a su vez sobre el nivel de respuesta de actividades tales como la alimentación, la dispersión, la puesta o el desarrollo.
En los últimos años, muchos investigadores se han interesado en la posibilidad de predecir los sucesivos eventos que tienen lugar a lo largo del ciclo de vida de los insectos.
De todos los factores ambientales, el que ejerce un efecto mayor sobre el desarrollo de los insectos es, probablemente, la temperatura. Ello es debido principalmente a su importante incidencia sobre los procesos bioquímicos, al ser organismos poiquilotermos, es decir, "de sangre fría". Por tanto, no es de extrañar que la idea de utilizar la temperatura y su influencia sobre el tiempo de desarrollo como instrumento de predicción, haya sido ampliamente utilizada (Wagner et al., 1984).
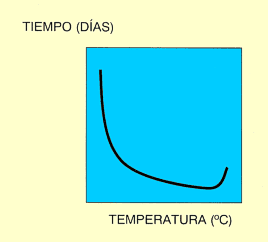
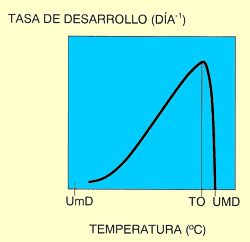
Como se ha señalado antes, la posibilidad de desarrollo de los insectos se da dentro de un rango determinado de temperaturas. Si se mide el tiempo de desarrollo utilizando valores puntuales próximos de temperatura y se representan los resultados en unos ejes cartesianos, aparece una curva en forma de "J" invertida (Fig. 1). Si lo que se representa en función de la temperatura es la tasa de desarrollo (definida como la inversa del tiempo de desarrollo y que, por tanto, mide la porción de desarrollo avanzada por unidad de tiempo), la curva resultante tiene forma sigmoidea (Fig. 2). Puede observarse cómo en el límite térmico inferior, la curva se aproxima al punto cero de desarrollo asintóticamente, porque los insectos sobreviven frecuentemente durante largos periodos de tiempo a bajas temperaturas con un desarrollo lento. Por esta razón, la temperatura a la que ocurre el desarrollo inicial (umbral mínimo de desarrollo), es difícil de medir con precisión. A medida que las temperaturas suben desde ese límite inferior, la tasa de desarrollo aumenta, pudiéndose ajustar la función a una recta, en la zona intermedia. Conforme nos acercamos a la temperatura óptima (aquella en que la tasa de desarrollo es máxima), el desarrollo comienza a ralentizarse, para caer después bruscamente. Además, a temperaturas superiores a la óptima, los porcentajes de mortalidad son muy elevados, lo que hace también difícil el estudio del desarrollo a altas temperaturas y, por tanto, la determinación del umbral máximo de desarrollo (temperatura por encima de la cuál el insecto no puede desarrollarse) (Pedigo, 1996).
 |
 |
|
Figura 1. Relación tiempo de desarrollo frente a temperatura. |
Figura 2. Relación tasa de desarrollo rente a temperatura. UmD: Umbral Mínimo de Desarrollo; TO: temperatura Óptima; UMD: Umbral máximo de Desarrollo. |
El método de grados-día como instrumento de predicción
A lo largo de los años, varios métodos se han basado en la relación tasa de desarrollo-temperatura, con fines predictivos. De todos ellos, el más extendido es el llamado método de grados-día. Los grados-día (ºD) representan la acumulación de unidades de calor por encima de cierta temperatura, durante un período de un día (en el caso de los insectos, esa cierta temperatura es el umbral mínimo de desarrollo). Para cada día se calculan, por tanto, como la diferencia entre la temperatura media diaria y el umbral mínimo de desarrollo:
ºD = temperatura media – temperatura umbral mínima
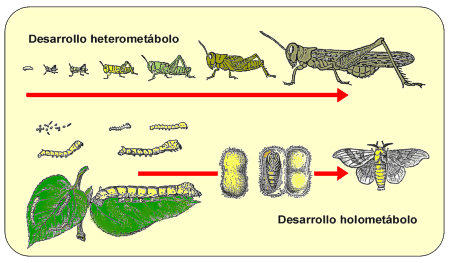
Figura 3. Diferentes eventos en insectos con desarrollo heterometábolo (arriba) y holometábolo (abajo). |
Para poder predecir el estado de desarrollo a partir de los grados-día, es necesario haber establecido antes, además del umbral mínimo de desarrollo, la integral térmica, definida como el número de grados-día que han de ser acumulados para que ocurra un evento determinado (eclosión, mudas larvarias o ninfales, pupación, emergencia del adulto -Fig. 3.-, etc.). De este modo, se puede estimar cuándo va a tener lugar ese evento, acumulando grados-día hasta alcanzar el valor de su integral térmica correspondiente.
La modelización de la relación "tasa de desarrollo-temperatura" como base para el cálculo de umbrales mínimos de desarrollo e integrales térmicas
Es un hecho que el umbral mínimo de desarrollo varía entre especies de insectos y entre estados y estadios. Del mismo modo, la integral térmica es diferente para eventos distintos y, entre especies diferentes, para un mismo evento.
Para la determinación de estos valores se han propuesto numerosos modelos empíricos y biofísicos que describen la relación tasa de desarrollo frente a temperatura. A continuación se hace una breve reseña de los principales modelos propuestos a lo largo del tiempo.
El primer modelo utilizado fue el Modelo Lineal. Basado en el trabajo de diversos autores (Candolle, 1885; Reibisch, 1902; Sanderson y Peairs, 1913; Arnold, 1960; Baskerville y Emin, 1969; Abrami, 1972; Allen, 1976, Sevacherian et al., 1977), asume como relación válida entre tasa de desarrollo y temperatura, la descrita por una recta. El umbral mínimo de desarrollo se determina tomando el valor del punto de corte de la recta con el eje de abscisas. Aunque es un modelo válido para temperaturas intermedias, no se ajusta a la realidad, tanto a temperaturas bajas como altas (ver Fig. 2), lo que impide un correcto cálculo de los umbrales mínimo y máximo de desarrollo, así como de la temperatura óptima y la integral térmica. No obstante, este modelo ha sido utilizado desde hace mucho tiempo por muy diversos autores dada su sencillez de cálculo y manejo y porque, en muchos casos, representa una aproximación aceptable.
Posteriormente, han ido apareciendo diversos modelos cuyo objetivo principal era el de resolver los problemas de que adolece el modelo lineal. Se describieron así los Modelos Catenario Simétrico y Asimétrico (Janisch, 1925), Exponencial (Belehradek, 1935) y Logístico (Davidson, 1944), ampliamente utilizados (sobre todo los dos últimos), pero también con problemas en los ajustes en las zonas de temperaturas altas y bajas. En 1974, Stinner et al. describieron el Modelo Sigmoide Modificado cuya aportación es la de corregir el desajuste de los modelos anteriores en la zona de altas temperaturas.
Todos los modelos citados hasta ahora son empíricos, ninguno de ellos basado en leyes biofísicas. En 1977, Sharpe y DeMichele formularon un complejo modelo biofísico que lleva su nombre y que es ampliamente aceptado y utilizado dado que describe correctamente la relación tasa de desarrollo-temperatura en todo el rango de desarrollo de la especie de insecto considerada.
Sin embargo, diferentes investigadores siguieron proponiendo modelos intentando, sobre todo, mejorar el cálculo del umbral mínimo de desarrollo. Así, en 1983, Hilbert y Logan describieron el Modelo de Logan tipo III, cuya expresión matemática es combinación de dos funciones. La primera para cubrir la parte ascendente de la tasa de desarrollo y la segunda para la región descendente de la misma. Con igual objetivo fue propuesto el Modelo de Lactin et al. (1995), cuya mejora con respecto al anterior es su mayor rigurosidad respecto a lo descrito matemáticamente por debajo del umbral mínimo de desarrollo; el modelo de Logan tipo III no es biológicamente correcto en este sentido, pues predice un aumento de la tasa de desarrollo a temperaturas inferiores a ese umbral, aspecto corregido en el modelo de Lactin et al.
En la actualidad se siguen estudiando modelos cuyo objetivo principal ha pasado a ser el de reducir el número de parámetros utilizados por el modelo. Así, en 1999, Briere et al. propusieron uno de sólo 3 parámetros que consigue muy buenos ajustes y permite seguir obteniendo el umbral mínimo de desarrollo.
Aplicaciones del método de grados-día
Poder predecir con fiabilidad la evolución estacional de los insectos es esencial para aspectos de interés diverso. Se destaca a continuación su aplicación en el Manejo Integrado de Plagas (MIP). Muchas de las decisiones que van a ser tomadas en los sistemas de MIP dependen del estado de las poblaciones de las plagas. Será clave por tanto, conocer dicho estado para aumentar las posibilidades de acierto en esa toma de decisiones. Se analizan a continuación dos ejemplos representativos de esta situación.
Son decisiones clave dentro del MIP, las relacionadas con la integración racional de los diferentes métodos de control al alcance en cada caso. La integración y aplicación correcta de esos múltiples métodos utilizables (mecánicos como la destrucción de residuos de cultivos, culturales como la elección de fechas de siembra, etc.) depende de un adecuado conocimiento del estado de la población de la plaga, por razones obvias.
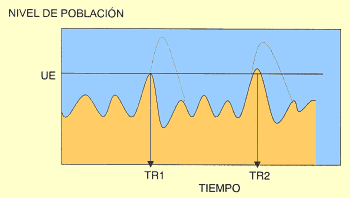
Figura 4. Evolución del nivel de población de una plaga, sin medidas de control (línea de puntos) y con ellas (línea continua). TR1: Tratamiento 1; TR2: Tratamiento 2. UE: Umbral Económico |
Otro aspecto crucial en el MIP es conocer cuándo la población plaga alcanza el Umbral Económico o Umbral de Acción, ya que dicho valor es la referencia para decidir llevar a cabo determinadas medidas de control de la plaga, por ejemplo, un tratamiento fitosanitario (Fig. 4). Pues bien, el Umbral Económico no es sino un nivel poblacional de la plaga que causaría daños económicos si no se actuase sobre ella, iguales al coste de las medidas de control. Por tanto, la toma de decisiones sobre actuar o no en función de este Umbral Económico requiere también de un preciso conocimiento del estado de la población.
Recomendaciones para la correcta aplicación del método de grados-día.
Restricciones de uso
Para una correcta aplicación del método de Grados-día es importante tener en consideración las recomendaciones siguientes:
! Todos los modelos de predicción de la tasa de desarrollo en función de la temperatura antes mencionados, se obtienen sometiendo poblaciones de la especie en cuestión, a temperaturas constantes en laboratorio. No se consideran por tanto, los ciclos diarios de temperatura que ocurren realmente en el campo. Han sido muchos los casos en que se han observado diferencias en los resultados cuando se han utilizado fluctuaciones de la temperatura a lo largo del día, incluso manteniendo las medias diarias iguales a las temperaturas constantes correspondientes. Por ello, diversos autores como Hangstrum y Milliken (1991) han propuesto métodos alternativos al de grados-día, para predecir el tiempo de desarrollo en condiciones de campo.
Los modelos que relacionan tasa de desarrollo y temperatura han de ser determinados para cada estado y estadio. Esto es debido a que dentro de una misma especie los valores de los umbrales de desarrollo y de las integrales térmicas pueden variar de modo muy significativo en cada uno de ellos. Por ejemplo, Marco et al. (1997) observaron que para Aubeonymus mariaefranciscae (Coleoptera, Curculionidae), el umbral mínimo de desarrollo oscilaba desde 5,6ºC para el primer estadio larvario, hasta más de 16ºC para el cuarto. Por tanto, no es correcto aplicar un valor único, ni siquiera para predecir el desarrollo completo.
Hay que destacar que todavía hay poca información disponible acerca de los requerimientos en grados-día de muchas especies. Este aspecto se agrava considerando que los datos obtenidos en poblaciones de una cierta localización geográfica pueden variar de modo sensible en lugares alejados de ella.
En vista de lo anterior, siempre que un método de grados-día vaya a ser utilizado como elemento de predicción, es conveniente hacer comprobaciones del grado de fluctuación de los valores de la tasa de desarrollo a una temperatura constante y a un ciclo diario de temperaturas cuya media coincida con la anterior. También es importante determinar los umbrales de desarrollo y los requerimientos en cuanto a integrales térmicas utilizando poblaciones de la zona donde se va a aplicar el método. Por último, siempre es interesante validar el modelo empleado, en condiciones de campo.
Por otro lado, aunque el método de grados-día ha sido y es utilizado con éxito en muchos casos, presenta una serie de restricciones que hacen que no siempre sea aplicable:
Es posible que en algún caso, otros factores ambientales tengan un efecto sobre el desarrollo que no sea despreciable respecto al efecto de la temperatura. Puede ser el caso de la humedad relativa o el fotoperiodo.
Existen limitaciones relacionadas con la precisión a la hora de acumular grados-día. Dichas limitaciones derivan principalmente de la medida de las temperaturas. Es frecuente que las medidas tomadas no representen con la precisión deseada, los valores reales a los que están sometidos los individuos de la población de insectos considerada.
Bibliografía
Abrami, G. 1972. Optimum mean temperature for plant growth calculated by a new method of summation. Ecology, 53: 893-900.
Allen, J. C. 1976. A modified sine wave method for calculating day degrees. Environ. Entomol., 5: 388-396.
Arnold, C. Y. 1960. Maximum-minimum temperatures as a basic for computing heat units. Proc. Am. Soc. Hort. Sci., 76: 682-692.
Baskerville, G. L. y Emin, P. 1969. Rapid estimation of heat acumulation from maximum and minimum temperatures. Ecology, 50: 514-517.
Belehradek, J. 1935. Temperature and living matter. Protoplasma Monogr. 8, Verlag Gebrüder Brontraeger. Berlín.
Briere, J. F., Pracros, P., Le Roux, A. Y. y Pierre, J. S. 1999. A novel model of temperature-dependent development for arthropods. Environ. Entomol., 28: 22-29.
Candolle, A. P. 1855. Geographique botanique, raisonée. París.
Davidson, J. 1944. On the relationship between temperature and rate of development of insect at constant temperatures. J. Anim. Ecol., 64: 26-38.
Hagstrum, D. W. y Milliken, G. A. 1991. Modeling differences in linsect developmental times between constant and fluctuating temperatures. Ann. Entomol. Soc. Am., 84: 369-379.
Hilbert, D.W. y Logan, J. A. 1983. Empirical model of nymphal development for the migratory grasshopper, Melanopus sanguinipes (Orthoptera, Acrididae). Environ. Entomol., 12: 1-5.
Janisch, E. 1925. Über die Temperaturabhängigkeit biologischer Vorgange und ihre Kurvenmassige Analyse. Pfluger's Archiv. Ges. Physiol., 209: 414-436.
Lactin, D.J., Holliday, N. J., Johnson, D. L. y Craigen, R. 1995. An improved rate model of temperature-dependent development by arthropods. Environ. Entomol., 24: 68-75.
Marco, V., Taberner, A. y Castañera, P. 1997. Development and survival of immature Aubeonymus mariaefranciscae (Coleoptera: Curculionidae) at constant temperatures. Ann. Entomol. Soc. Am., 90: 169-176.
Pedigo, L. 1996. Entomology and pest management. 2nd Edition. Ed. Prentice-Hall Inc. New Jersey. 679 pp.
Reibisch, J. 1902. Über den Einfluss der temperatur auf die Entwicklung von fischeiern. Wiss Meeresuntersuch., 2: 213-231.
Sanderson, E. D. y Peairs, L. M. 1913. The relation of temperature to insect life. N.H. Coll. Agric. Exp. Stn. Tech. Bull. Nº 7.
Sevacherian, V., Stern, V. M. y Mueller, A. J. 1977. Heat accumulation for timing Lygus control measures on a safflower-cotton complex. J. Econ. Entomol., 70: 399-402.
Sharpe, P. J. H. y DeMichele, D. W. 1977. Reaction kinetics of poikilotherm development. J. Theor. Biol., 64: 649-670.
Stinner, R. E., Gutiérrez, A. P. y Butler, G. D. 1974. An algorithm for temperature-dependent growth rate stimulation. Can. Entomol., 106: 519-524.
Wagner, T.L., Wu, H., Sharpe, P. J. H., Schoolfield, R. M. y Coulson, R. N. 1984. Modeling insect development rates: a literature review and application of a biophysical model. Ann. Entomol. Soc. Am., 77: 208-225.